ماتریس سختی کل در درس روش المان (اجزای) محدود یکی از بخش های حیاتی برای یافتن مجهولاتی مانند تنش، کرنش، نیروی تکیه گاهی و دمای نقاط مختلف یک سیستم جامداتی می باشد.
خرپا ساده ترین سازه مکانیکی است. برای تحلیل پارامترهای مورد نظر باید گام های زیر را به ترتیب پی نمود:
- انتخاب المان مناسب
- المان بندی (جدول Connectivity)
- محاسبه ماتریس های سختی و نیرویی برای هر المان
- مونتاژ کردن (Assembling) در نهایت بدست آوردن سختی و نیرو در دستگاه جهانی
- اعمال شرایط مرزی (به روش حذف یا پنالتی)
- KQ = F
- تحلیل تنش، کرنش، جابه جایی و نیروی تکیه گاهی
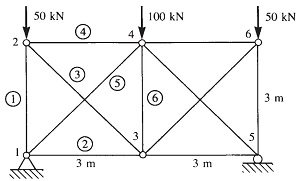
در خرپای نشان داده شده در شکل بالا 6 گره و 11 المان وجود دارد. درجه آزادی هر گره با توجه به دوبعدی بودن مساله، دو است. بنابراین ماتریس سختی کل 12 در 12 خواهد بود.
حالت اول: آرایه روی قطر اصلی
برای مثال آرایه K33 در این ماتریس کلی به شرح زیر بدست می آید.
در صورت زوج نبودن یک واحد به عدد اندیس اضافه می کنیم، سپس تقسیم بر دو می کنیم. داریم:
2=2/(3+1)
پس المان های متصل به گره دوم در آرایه ماتریس سختی کل مدنظر وجود دارد، به این صورت که:
K33 = K(1) +K(3) + K(4)
به گره دوم المان های 1، 3 و 4 وصل می باشند.
حال باید ببینیم درجه آزادی 33 در کجای ماتریس سختی این المان ها وجود دارد؟
در صورت ترتیب به صورت پادساعتگرد داریم:
المان 1: K11
المان 3: K33
المان 4: K33


دیدگاهها (0)